教科の紹介　詳細 | 鳴門教育大学附属中学校

数学

令和６年度数学科研究授業③

1月27日（月）に、長年本校でご勤務された経験をお持ちの学力調査官の先生をはじめ、多数の先生方に授業を見ていただき、ご指導・ご助言を賜りました。「確率の利用」の学習において、「ワイルドカードシリーズで、2戦目と3戦目のどちらのチケットを購入すれば、優勝シーンを見られる可能性が高くなるのか」について考えました。樹形図を用いて起こる場合の数を考え、2戦目と3戦目で優勝シーンが見られる確率をそれぞれ求め、問題を解決することができました。考えが分かれた解法について、これまでの既習事項を関連付けながら議論することができました。さらに、その問題を発展させ、「全5試合で行われる地区優勝シリーズにおいては、何戦目のチケットを買えばよいのか」という問いについても考え、学習内容の理解を深めることができました。

令和６年度数学科研究授業②

　1月27日（月）に、長年本校でご勤務された経験をお持ちの学力調査官の先生をはじめ、多数の先生方に授業を見にきていただき、ご指導・ご助言をいただきました。

　第２学年の「図形の性質と証明」の学習では、正三角形を題材に三角形の合同条件を用いた証明を行いました。生徒は実際に図をかき、その図の中の２つの線分が等しいという推測をし、その推測が成り立つことを証明しました。生徒たちが協力しながら新たな性質を見いだそうとするなど、主体的に学習に取り組んでいる姿が見られました。さらに、学力調査官をはじめ、多くの先生方が参加してくださり、生徒の取組を見守っていただきました。今後も本校の数学科では、生徒一人一人の学力向上と授業の質の向上を目指すため新たなアプローチを模索してまいります。

令和６年度数学科研究授業①

　1月28日（火）に、長年本校でご勤務された経験をお持ちの学力調査官の先生をはじめ、多数の先生方に授業を見にきていただき、ご指導・ご助言をいただきました。

　第１学年の「空間図形」の学習では、立方体の切断面が正方形になるかひし形になるかを考察する授業を行いました。直観的に判断したことを図形の性質や、展開図、投影図等の既習の知識を用いることで様々な視点から課題を解決し、論理的に説明しようとする生徒の姿を見ることができました。当日の研究授業では、生徒たちが真剣に授業に取り組む様子を観察いただき、多くの貴重なフィードバックをいただきました。また、先生方も生徒の取り組みを見守りながら、授業内容の評価と改善点について議論を深める機会となりました。今後も、教育の質を高めるための取組を続けてまいります。

「中点連結定理の利用の学習」（３年生）

「中点連結定理の利用の学習」において、「四角形の４つの辺の中点を結んでできる四角形は、どのような四角形になるのか」ということについて考えました。まず、実際に図形をかくことを通して、その四角形が平行四辺形になりそうであることを予想し、それが成り立つことを証明しました。分からないところを教え合ったり、既習事項と関連付けたりしながら取り組む生徒の姿が見られました。さらに、その問題を発展させ、「元の四角形にどのような条件を加えれば、中点を結んでできる四角形はひし形になるのか？」ということについて問いかけ、その問いに対しても、周囲と協力して取り組み、統合的・発展的な考察をすることができました。

また、この授業はカリブ海沿岸の国々から、小・中・高の算数・数学の先生方が視察をしに来られた授業でもあり、たくさんの人に見られながらも、いつも通り主体的に取り組むことができていました。

「関数ｙ＝ａｘ²」についての学習（３年生）

　「関数ｙ＝ａｘ²の利用」の分野において、アニメ「アルプスの少女ハイジ」のＯＰの中で、ハイジが乗っているブランコの長さを求めるという学習を行いました。はじめに、ＯＰの映像を見て、「気になることは何かありますか？」と聞いたところ、「ブランコの長さが長くて、怖そう。」という発言が多くありました。そこから、本時の問題を設定し、解決に向けて、振り子の実験しながら、長さを求めました。自分たちの気になることを問題として取り上げ、学んだ数学を活用しながら、班で協力して取り組む附中生の姿がとても素晴らしかったです。以下は、授業の感想（抜粋）になります。

○今日は振り子の考え方を用いて、ハイジの乗っているブランコの長さを求めた。想像していたよりも少し短かったが、数学的にアニメの世界の物事を解明するのはとても面白いと感じた。

○関数を使うことで、実際には分かりにくいものも数値で求められることが分かった。関数ｙ＝ａｘ²など新たな関数を習ったことで様々な問題を解けるようになったことを実感した。

「比例・反比例の利用」についての学習（１年生）

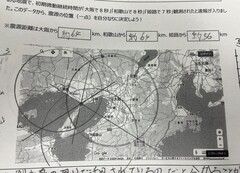
　1年生「比例・反比例の利用」において、初期微動継続時間と震源距離の関係を明らかにする授業を行いました。はじめに、「緊急地震速報について気になることはありませんか？」と聞き、地震がなぜ予測できるのかを生徒に問いました。そこから「初期微動継続時間が分かれば、震源距離が求まる」という関数関係に着目し、実際のデータを使いながら、比例とみなせることに気づくことができました。最後には、与えられた初期微動継続時間だけで震源距離を求め、地図上からおよその震源地を特定するということができるようになりました。これまでの、関数における表・式・グラフを活用し様々な視点から問題解決している生徒の姿が見られました。以下は、授業後の感想です。（抜粋）

○知らないだけで日常にも比例を使うところがあるんだなと感じました。ほかにも比例が使われているものを調べていきたいです。

○１つ１つ計算をしていくと、比例とみなせた。比例と捉えることでほかの地震での震源距離を求めることができたので便利だと感じた。

○自分の身近なものに比例の関係があることを知れました。また、このような知識を少しでも持っているだけでいざというときに役立つのかなと思いました。

「二次方程式」についての学習（３年生）

　３年生で二次方程式の単元において、「解の公式」を明らかにする授業を行いました。解の公式が成り立つ理由を考えるのは難しい内容ですので、インターネットで調べたり、学習班で教え合いをしたりしながら、学習を進めていきました。班で協力して、難易度の高い学習活動に取り組む姿がとてもよかったです。以下は、授業後の感想です。（抜粋）

●解の公式が成り立つか証明しました。自力ではなかなかわかりませんでしたが、ネットで調べてみると様々なやり方があり面白かったです。また、ａ≠０というところがすごく上手にできているなと思いました。ａが０の可能性があるなら、この証明は成り立たないし、そもそも二次方程式は成り立ちません。そのことを改めて理解し、数学の面白さを知りました。解の公式が成り立つと証明することができたことで、公式を使えるようになったのでよかったです。

●今日の学習では、解の公式の証明をした。今まで解の公式の成り立ちを知らず、公式だけを覚えて問題を解いていたが、今回インターネットで調べながら解の公式の証明をしたことで、二次方程式や解の公式への理解が深まった。これからも解の公式だけでなく、色々な公式が「どうやってこうなったのか」ということを考えながら数学の学習を進めていきたいと思う。

「多角形の内角の和」についての学習（２年生）

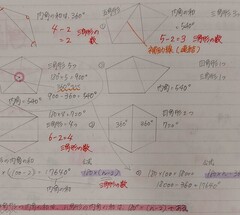
　２年生「図形の調べ方」において、「多角形の内角の和」の学習を行いました。三角形の内角の和が１８０°であることを用いて、四角形や五角形、六角形の内角の和を求めました。さらに、「百角形の内角の和は何度であるか。」という問いに対しては、四角形や五角形、六角形のときの考え方やそれらの結果を用いて解決を進めました。解決を通して、「帰納的に考える」や「類推する」等の数学的な考え方を働かせることの大切さに気付いている姿や、さらに、「未知の図形であっても自分たちの知っている形に置き換えることが解決につながる」ということを改めて実感している姿が見られました。これらの姿は、今回の問題にとどまらず、別の問題を解くときにおいても生かされると考えます。引き続き、数学科としては、次の問題解決につながるような授業展開を日々行っていきたいと思います。

「乗法の公式」についての学習（３年生）

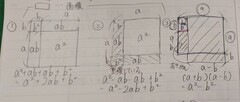
　３年生「式の展開と因数分解」において、「乗法の公式」の学習を行いました。まずは、「乗法の公式」を板書に示した後、「この公式を知っていると展開が簡単に速くできる」という意見が出され、乗法の公式の必要性について全体で確認しました。また、前回の学習で出された「面積図」を用いて考えることで、乗法の公式について視覚的に理解を深めることができました。特に、和と差の積の公式の面積図（写真右）に感動している姿がよく見られました。

令和６年度数学科研修①

　4月18日（木）に鳴門教育大学の藤原先生に授業を見にきていただき、ご指導・ご助言をいただきました。2年生と３年生で授業を行い、藤原先生より様々な視点からアドバイスをいただき、とても勉強になりました。教えていただいたことを大切にしながら、我々の授業をブラッシュアップし、引き続き、生徒にとって「よく分かる授業」ができるよう、研鑽に励んでいきたいと思います。次は、５月３１日（金）の研究発表会に向けて、数学科一丸となって教材研究に取り組んでいきたいと考えています。

「式の計算と因数分解」についての学習（３年生）

　３年生「式の展開と因数分解」において、「多項式どうしの乗法」の学習を行いました。前時には、多項式と単項式の乗法・除法について分配法則に基づいて計算することを学びました。今回も新しい形の式ではありますが、前時の内容を生かして、「多項式どうしの乗法」を「多項式と単項式の乗法」に変えて計算を進めることができました。また、面積図で考える方法についても理解を深めることができました。以下に、生徒のみなさんの感想を一部紹介します。

・○さんの説明を聞いて、難しい式でも前に習った形に変えると、わかりやすいと感じました。もう少し自分でくわしい説明ができるようにしたいです。

・これからも新しい問題を解くときは、前回の内容を生かして解きたいです。

・面積図を用いて視覚的に考えることも分かりやすいと思いました。

タブレット端末を用いての問題演習

　数学科では、基礎・基本の定着や個別学習の充実に向けて、アプリケーションを利用して問題を配付し、生徒が自分のペースで問題演習をしていく時間を授業の中に時折、設定しています。２月の中旬には１、２年生でも県下一斉のテストである基礎学力テストが実施されます。その対策として、過去問をアプリケーションから配信し、問題を解く時間を設定しました。生徒たちは、真剣な表情で既習内容を思い出しながら、しっかりと取り組んでいました。集中して粘り強く問題を解く生徒の姿にとても感心しています。みなさん、テスト本番も頑張ってね。

「正多面体」についての学習（１年生）

　第１学年の空間図形の単元において、「正多面体」について授業を行いました。ポリドロンという４色8種類の幾何学的な形で平面的な模様や立体を作ることができる教具を用いて、「正多面体は５種類しか存在しないこと」を明らかにしました。具体物を用いて考えることで、生徒の理解も深まりました。また、オイラーの多面体定理にもふれることで、発展的な学習を生徒とつくりあげることができました。

「図形の相似『中点連結定理』」についての学習（３年生）

　第３学年の「図形の相似『中点連結定理』」について授業を行いました。錯視（ある図形の大きさや長さなどが，周囲の図形の影響を受けて実際とは違って見えること。）の図を見せ、図中の２つの線分の長さの関係について考えました。生徒は実際に図を見て判断したことと、それとは違う結果であることに驚き、意欲を高めながら、学習に取り組んでいました。その中で、「三角形の相似」や「平行線と線分の比」の内容を関連付けながら、２つの線分の長さが等しいことを証明し、問題を解決しました。学習を通して、錯視に興味をもつつとともに、中点連結定理の存在を知り、その定理が成り立つ理由について理解することができました。右に生徒のノートを紹介します。

「基本の作図」についての学習（１年生）

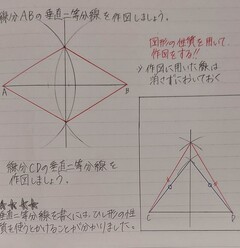
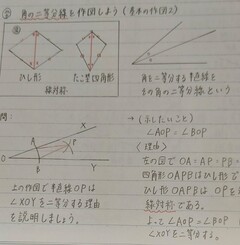
　第１学年の「基本の作図」について授業を行いました。作図の手順を覚えることも大切ですが、図形の性質を根拠に作図について学ぶことを大切に授業を行いました。生徒は、ひし形の性質や線対称な図形の性質を関連付けながら、作図について、理解を深めることができました。右に、生徒のノートを紹介します。

「方程式の利用」についての学習（１年生）

　第１学年の「方程式の利用」の第１次の授業を行いました。今回は、本校教頭の東條みどり先生が、本校数学科の教員及び、教育実習の先生に向けて、師範授業をしてくださいました。「Aさんが５３歳で、Bさんが１３歳であるとき、Aさんの年齢がBさんの年齢の３倍になるのは、何年後になるかを求めましょう。」という問題に取り組みました。まず、小学校で学習した算数を用いて問題を解決した後、方程式を利用して問題を解決し、方程式を利用することのよさについて考えました。生徒とやりとりをしながら学習内容について深く理解することを促したり、分かりやすい説明や板書をしたりするみどり先生の姿から、我々教員もたくさんのことを学ばせていただく時間となりました。

一次関数「変化の割合」についての学習（２年生）

　第２学年の「一次関数」の単元において，変化の割合についての授業を行いました。電気ポットでお湯を沸かしたとき，沸かしはじめてから２分～５分の間と５分～９分の間では，どちらが温度の上がり方は急であるかという問題について考えました。その問題を通して，「変化の割合」について理解することができました。さらに，変化の割合を求めていく練習問題を通して，一次関数の変化の割合は一定であることを見いだし，それを文字を用いて説明しました。この説明では，（多項式）÷（多項式）の処理が入り，高校数学の内容にもふれました。また，授業の終わりには，反比例の変化の割合は一定であるかどうかについて考えました。中２の内容だけでなく，中１，高校の内容も盛り込んだ授業になりました。前年の内容を学び直したり，発展的な内容を学習したりすることで，学びに対する満足感や充実感を得ている姿が見られました。今後もそのような姿を目指し，夏休み期間を大いに活用し，数学科チーム一丸となり，教材研究に励んでいきたいです。

「正の数・負の数の乗法」についての学習（１年生）

　正の数・負の数の乗法についての学習をしました。（正の数）×（負の数）や（負の数）×（負の数）などの計算について，それらが成り立つ理由を今まで学習した知識を使って明らかにしました。計算の仕方を覚えて，速く計算することも大切ですが，その理由を明らかにし，様々な知識について，その概念まで深く理解することも大切に授業を行っています。以下に，生徒のみなさんの感想やノートの一部を紹介します。

「友達の意見を聞いていると，みんなそれぞれ考え方が違い，一つの答えを求めるのにも，様々な求め方があるのだと思いました。」，「自分は数直線で考えたけど，○○さんは乗法を加法に直して考えていました。今までに習った正の数・負の数の加法の学びを使っていてすごいと思いました。」，「自分では考えつかなかったことがたくさんでてきて，すごく分かりやすい解説でした。自分の考えは，他の人と比べ分かりにくかったので，次のときは，発表してくれた人のような分かりやすい説明がしたです。」など。

「平方根の利用」についての学習（３年生）

　第３学年の「平方根の利用」で，丸太と角材の関係について考える授業を行いました。丸太の断面を円とみて，「直径△ｃｍの丸太から，切り口ができるだけ大きい正方形の角材を切りとるとき，正方形の１辺の長さは何ｃｍになるか」という問題に取り組みました。問題を解決した後は，丸太の直径と正方形の一辺の長さの関係を見いだし，そのことを用いて，さしがねの目盛りのしくみについて考えました。さしがねのしくみに関心をもつ姿や，身近な道具にも平方根の考えが潜んでいることに数学の有用性を感じている姿などが見られました。

令和５年４月２３日（日）参観授業

　３年生「式の展開と因数分解」において，「速算法」の学習を行いました。ある条件における２けた自然数同士の乗法は，筆算で行うことよりも，しくみを知っていれば速く計算することができます。そのしくみがなぜ成り立つのかということについて，既習内容を関連付けながら考察しました。以下に，生徒のみなさんの感想を一部紹介します。

　「文字において正しいかどうかの証明をすることが楽しかったです。」，「結論を導くために式を変形していくのがおもしろかったです。」，「はじめ，私は文字を２種類使って処理をしていましたが，別の考えを聞いて３種類使って処理をした方がやりやすいと思いました。」，「他の速算法も調べてみたいです。」など。